Lucrarea nr.8:

Curbe de aproximare si interpolare:
Curbe B-Spline cubice

[ Prev ] Lucrarea 8 [ Next ]

Descriere

Implementare

Aplicatii

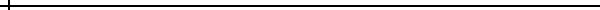
A.Descriere

1. Curbe B-Spline cubice

In grafica pe calculator curbele trebuie sa indeplineasca o serie de conditii. Este de dorit ca acestea sa aibe un aspect regulat, neted, fara discontinuitati, oscilatii sau bucle intre punctele de control. Totodata, influenta punctelor asupra aspectului general al curbei trebuie sa fie limitata in sensul ca modificarea pozitiei unui punct de control trebuie sa aiba un efect local, schimband aspectul curbei numai intr-o vecinatate restransa a punctului respectiv. Aceasta proprietate a curbei poarta denumirea de control local si permite proiectarea interactiva a formelor obiectelor prin incercari repetate.

Totodata, este de dorit ca ecuatiile analitice ale curbelor sa fie cat mai simple. In general se utilizeaza curbe descrise prin functii polinomiale de grad redus (2 sau 3). O astfel de curba nu va putea acoperi intregul set de puncte de control. Solutia consta in separarea setului de puncte de control in subgrupe de puncte si construirea unor curbe de grad redus pentru fiecare subgrupa. Curba cautata va rezulta din asamblarea acestor curbe elementare (portiuni de curba) si deci ea nu va fi descrisa de o ecuatie unica pe intregul domeniu de definitie. Aspectul neted al curbei rezultate va fi obtinut prin impunerea conditiilor de continuitate si derivabilitate functiei asociate, in punctele de jonctiune a doua portiuni de curba.

Construind in acest mod curbe de interpolare, utilizand curbe descrise de functii polinomiale de grad 3 se obtine curba spline cubica naturala. Dezavantajul acesteia este controlul global pe care il exercita fiecare punct de control asupra curbei. Determinarea acestei curbe avand n+1 puncte de control necesita rezolvarea unui sistem liniar de 4*n ecuatii cu 4*n necunoscute. Acest sistem furnizeaza coeficientii functiilor polinomiale de grad 3 asociate celor n portiuni de curba care definesc curba de interpolare.

O alta metoda pentru constructia unei curbe de interpolare spline cubica utilizeaza un set de curbe SPLINE DE BAZA. Curba de interpolare se obtine ca o combinatie liniara (suma ponderata) a acestora. Si in acest caz se obtine o curba de interpolare asupra careia fiecare punct de control exercita o influenta globala.

Asigurarea controlului local asupra unei curbe spline cubice de interpolare nu pot poate fi obtinuta decat renuntand la unele conditii asupra curbei. Renuntand la cerinta ca curba sa treaca prin punctele de control conduce la obtinerea unor curbe de aproximare numite CURBE B-SPLINE CUBICE (figura 1). Renuntand la cerinta de derivabilitate de ordin II a curbei, se va obtine o curba de interpolare de tip Romm-Catmull (figura 2).

Curbele B-Spline cubice sunt formate prin combinatii liniare ale unor curbe spline numite B-Spline sau baze. Curba B-Spline cubica este in general si ea o curba spline.

Pentru reprezentarea acestui tip de curba se utilizeaza o forma parametrica. Fiind date n+1 puncte de control, P₀, …,P_n, vom diviza intervalul [0,n] al parametrului u in n subintervale [u_i, u_i+1], cu 0 <= t <= 1 si t(0)=u_i si t(1)=u_i+1. Pentru fiecare subinterval avem, in expresia matriceala:

figura 1

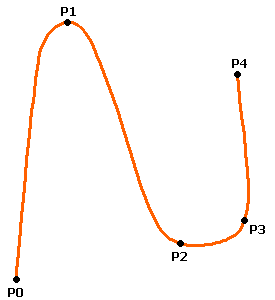
figura 2

pentru curbele B-Spline cubice, respectiv

pentru curbele Romm-Catmull.

Un punct al curbei va avea coordonatele [c_x(t), c_y(t)], obtinute aplicand formula de mai sus si inlocuind vectorul P cu coordonatele x respectiv y ale punctelor de control.

2. Proprietatile curbei B-Spline cubice

• curba nu este o curba de interpolare ci una de aproximare
• specificand un punct de control de doua ori, curba este atrasa mai aproape de acel punct
• specificand un punct de control de trei ori, curba trece prin acel punct

B. Implementare

Se va completa modulul G2Dcurbe cu rutine necesare trasarii curbelor de aproximare B-Spline cubice, respectiv a curbelor de interpolare Romm-Catmull:

/*======================================================================*/
/* Completari la G2Dcurbe.h                                             */
/*======================================================================*/

typedef enum
{
   B_SPLINE,
   ROMM_CATMULL
} TIP_CURBA;

/*
 * Traseaza curba B_spline cubica, respectiv curba Romm-Catmull
 * pornind de la un set de puncte de control specificate in
 * fisierul "nume_set". Fiecare segment de curba este aproximat prin
 * "ns" segmente de dreapta.
 */
extern void curba_b_spline (char *nume_set, TIP_CURBA t, int ns);

/*======================================================================*/

/*======================================================================*/
/* Completari la G2Dcurbe.c                                             */
/*======================================================================*/

/* Tipuri si Structuri Private -----------------------------------------*/

typedef double VECTOR[4];
typedef double T_MAT[4][4];


static VECTOR vx, vy;
static T_MAT m;


/* Prototipuri Private -------------------------------------------------*/

/* Formeaza matricea transformarii */
static void form_mat (TIP_CURBA t, T_MAT m);

/* Traseaza curba spline */
static void plot_spline (int ns);

/*
 * Formeaza vectorii cu coordonatele punctelor de control pentru
 * segmentul de curba "i"
 */
static void calc_vectori (int i);

/* Traseaza un segment de curba prin aproximare cu "ns" segmente */
static void plot_c (int ns);

/* Implementeaza produsul matricial din relatia (1) */
static void mult (VECTOR x, T_MAT m, VECTOR y);


static double det (VECTOR v, double t);


/* Rutine Publice ------------------------------------------------------*/

/*
 * Traseaza curba B_spline cubica, respectiv curba Romm-Catmull
 * pornind de la un set de puncte de control specificate in
 * fisierul "nume_set". Fiecare segment de curba este aproximat prin
 * "ns" segmente de dreapta.
 */
void 
curba_b_spline (char *nume_set, TIP_CURBA t, int ns)
{
   citeste_puncte (nume_set);
   form_mat (t, m);
   plot_spline (ns);
} /* curba_b_spline */




/* Rutine Private ------------------------------------------------------*/

/* Formeaza matricea transformarii */
static void 
form_mat (TIP_CURBA t, T_MAT m)
{
   double a = 0.0;

   if (B_SPLINE == t)
   {
      a = 1.0;
   }

   m[0][0] = 2.0*a-3.0; m[0][1] = -6.0*a+9.0; m[0][2] = -m[0][1]; m[0][3] = -m[0][0];
   m[1][0] = -3.0*a+6.0; m[1][1] = 9.0*a-15.0; m[1][2] = -9.0*a+12.0; m[1][3] = 3.0*a-3.0;
   m[2][0] = -3.0; m[2][1] = 0.0; m[2][2] = 3.0; m[2][3] = 0.0;
   m[3][0] = a; m[3][1] = 6.0-2.0*a; m[3][2] = a; m[3][3] = 0.0;

} /* form_mat */




/* Traseaza curba spline */
static void 
plot_spline (int ns)
{
   int i;

   for (i = 1; i < lista.n-2; i++)
   {
      calc_vectori (i);
      plot_c (ns);
   }
} /* plot_spline */



/*
 * Formeaza vectorii cu coordonatele punctelor de control pentru
 * segmentul de curba "i"
 */
static void 
calc_vectori (int i)
{
   VECTOR x, y;
   int j;

   for (j = 0; j < 4; j++)
   {
      x[j] = lista.x[i+j-1];
   }
   mult (x, m, vx);
   for (j = 0; j < 4; j++)
   {
      y[j] = lista.y[i+j-1];
   }
   mult (y, m, vy);
} /* calc_vectori */


/* Traseaza un segment de curba prin aproximare cu "ns" segmente */
static void 
plot_c (int ns)
{
   double t, t1, t2;
   double delta;
   double x1, y1, x2, y2;
   int i;

   t1 = 0.0; t2 = 1.0;
   x1 = det (vx, t1); y1 = det (vy, t1);
   delta = (t2-t1) / ns;
   t = t1;
   for (i = 0; i < ns; i++)
   {
      t += delta;
      x2 = det (vx, t);
      y2 = det (vy, t);
      linie_2d (x1, y1, x2, y2);
      x1 = x2; y1 = y2;
   }
} /* plot_c */




/* Implementeaza produsul matricial din relatia (1) */
static void 
mult (VECTOR x, T_MAT m, VECTOR y)
{
   int i, j;

   for (i = 0; i < 4; i++)
   {
      y[i] = 0.0;
      for (j = 0; j < 4; j++)
      {
         y[i] += m[i][j] * x[j];
      }
   }
} /* mult */


static double 
det (VECTOR v, double t)
{
   double result;

   result = (v[0]*t*t*t + v[1]*t*t + v[2]*t + v[3]) / 6.0;

   return (result);
} /* det */

/*======================================================================*/

C. Aplicatii

1. Implementati procedurile pentru trasarea curbelor spline.
2. Tinand cont de proprietatea curbelor B-Spline cubice de a fi continute in poligonul convex determinat de punctele de control, scrieti o procedura pentru determinarea unei ferestre minime care sa incadreze curba. Reprezentati sistemul de axe de coordonate.
3. Pentru fiecare din seturile urmatoare de puncte de control reprezentati curbele B-Spline cubice si Romm-Catmull:

1. (0,0), (5,10), (15,15), (20,15), (25,12), (27,10), (24,8), (18,0), (15,-4), (10,-8), (15,-10), (20,-20), (25,-15), (30,-10), (35,0)
2. (2,0), (4,0), (4,2), (4,4), (2,4), (10,4), (0,2), (0,0)
3. (0,0), (2,0), (4,0), (4,2), (4,4), (2,4), (0,4), (0,2), (0,0), (2,0), (4,0).

Urmariti efectul asupra curbei daca:

• punctul (4,4) se inlocuieste cu punctul (6,6)
• punctul (4,4) se specifica de doua ori succesiv
• punctul (4,4) se specifica de trei ori succesiv

[ Home ][ Up ][ Previous ][ Next ]

Send mail to sorin@aspc.cs.utt.ro with questions or comments about this web site.
Copyright © 2000 Graphics Laboratory
Last modified: