APLICATII : ALGORITMI - RECURSIVITATE

(1) Labirint 3D

Pentru problema de determinare a tuturor solutiilor de iesire dintr-un labirint 3D: sa se scrie un program pentru determinarea tuturor solutiilor si a optimului de iesire dintr-un labirint tridimensional.

(2) Reconstructia punctelor

Exista n puncte, p1, p2, ..., pn, toate localizate pe axa x, iar xi este coordonata lui pi. Se presupune ca x1=0 si punctele sunt numerotate de la stanga la dreapta. Aceste n puncte determina n*(n-1)/2 distante (de valori nu neaparat unice), d1, d2, ....,dm intre oricare 2 puncte distincte xi si xj.

Problema reconstructie este urmatoarea: se dau m valori, (sortate in ordine crescatoare), care reprezinta setul de distante intre m=n*(n-1)/2 perechi de puncte. Se cere sa se reconstituie coordonatele celor n puncte.

(3) Taieturi

Sa se scrie un program care sa gaseasca toate variantele, precum si cea optima pentru taierea unui fir de lungime L in parti de lungimi L1,L2,...,Ln date, in conditiile:
a)nu exista nici un fel de restrictie in ce priveste numarul de bucati din fiecare lungime
b)se taie cel mult o bucata de fiecare lungime
c)numarul de bucati de fiecare lungime sa difere prin cel mult o unitate

(4) Formatare de text

Se considera urmatoarea problema de formatare a textului unui paragraf, care este o secventa de n cuvinte, c1, c2, ..., cn, de lungimi a1, a2, ..., an, care trebuie afisate pe linii de lungime L. Cuvintele trebuie separate prin spatii, a caror lungime ideala este b, dar spatiile pot fi extinse sau comprimate (dupa comprimare trebuie sa ramina totusi > 0), astfel incat o linie ce contine cuvintele ci ci+1 ... cj sa ocupe exact lungimea L. Pentru fiecare spatiu b' care este este mai mare sau mai mic decat lungimea ideala b, se defineste un "gradul de uratenie" ca fiind |b' - b|. Pentru intregul paragraf, este de dorit ca suma acestor grade de uratenie sa fie minim. Se cere sa se scrie programul care determina valorile lungimilor spatiilor separatoare astfel incat sa se obtina o formatare cat mai estetica a textului.

(5) Recursivitate

Sa se scrie cite o procedura recursiva pentru:
a)transformarea unui intreg din baza 10 in alta baza data
b)tiparirea nodurilor unei liste in ordine inversa
c)analog cu b), dar pentru elementele unui tablou
d)copierea in ordine inversa a liniilor dintr-un fisier text, in altul.

(6) Alcatuire chestionare

Se considera un set de N intrebari, fiecare avand un punctaj Pi. Sa se genereze toate chestionarele continand un numar de intrebari intre A si B si avand un punctaj total intre C si D.

(7) Triunghi magic

Se considera un triunghi format din n linii, pe fiecare linie i sunt i numere intregi pozitive, ca in exemplul de mai jos:

                 7
             3        8
         8       1        0
      2      7        4      4
   4      5      2        6      5

Exemplu: pentru triunghiul de mai sus, drumul cautat este: 7 - 3 - 8 - 7 - 5

(8) Labirint culori

Se considera o suprafata caroiata de dimensiune n x n, in care fiecare patrat are una din culorile: galben, rosu, albastru sau verde. Configuratia suprafetei se citeste de la tastatura ( sau dintr-un fisier ). Sa se determine si sa se tipareasca daca exista drumuri ( minime ) intre colturile opuse - un drum trebuie sa cuprinda doar patrate de aceeasi culoare; deplasarea dintr-un patrat se poate face in oricare din cei opt vecini.

(9) Cablaj

Pe un circuit electric trebuie plasate n componente. Plasarea lor se face in n pozitii bine determinate, identificate cu numerele 1.. n. Se da o matrice c in care c[i,j] reprezinta numarul de conexiuni care trebuie facute intre componentele i si j, precum si o matrice d, cu d[p,q] reprezentind distanta intre punctele p si q. Cablarea consta in plasarea fiecarei componente intr-o anumita pozitie. Nu se pot aseza 2 componente in aceeasi pozitie. Costul cablarii este suma valorilor c[i,j]*d[p,q], unde componenta i a fost plasata in pozitia p iar componenta j in pozitia q.

Se cere sa se determine o plasare a componentelor pe pozitii astfel incit costul total al cablarii sa fie minim.

Fisierul de intrare, cu numele citit de la tastatura, contine:
- pe prima linie valoarea lui n
- pe urmatoarele n linii elementele liniilor lui C
- pe urmatoarele n linii elementele liniilor lui D

Iesirea va consta in afisarea permutarii care duce la costul minim, in forma: pozitia 1 - componenta x; pozitia 2 - componenta y ......

(10) Orarul cursurilor

Sa se scrie un program care sa vina in sprijinul alcatuirii orarului cursurilor facultative. Exista un numar de N=20 cursuri si M=100 studenti. La inceputul anului, fiecare student isi exprima optiunea privind cursurile la care doreste sa participe. Un student poate alege un numar oarecare de cursuri (0 ..N), dar in medie numarul cursurilor alese este de 2-3.

Problema responsabilului cu alcatuirea orarului este de a identifica care sunt cursurile care pot fi programate a se desfasura in paralel. Se pot desfasura in paralel 2 sau mai multe cursuri, cu conditia sa nu existe suprapuneri in orarul nici unui student.

Programul va citi din fisierul s.dat numarul N de cursuri, numarul M de studenti, si apoi, pentru fiecare student, pe cite o linie, cursurile la care este insctis acesta. Programul determina grupele de cursuri care se pot desfasura in paralel(o varianta).

Exemplu:

N=5, M=6
studentul 1 alege cursurile 1,2
studentul 2 nu alege nimic
studentul 3 alege cursurile 1,3
studentul 4 alege cursul 4
studentul 5 alege cursul 4
studentul 6 alege cursul 5

Observatie: se recomanda folosirea unui tip "multime de cursuri": Fiecare student are o multime de cursuri la care s-a inscris. Pe baza acestora, se poate determina, univoc, pentru fiecare curs, multimea cursurilor cu care este "in conflict", iar apoi evitind conflictele, se poate da o solutie de grupare a cursurilor.

(11) Drum minim

Intre n orase exista o retea de drumuri care permite ca dintr-un oras sa se ajunga in oricare din celelalte. Intre 2 orase exista cel mult un drum direct, de lungime cunoscuta, iar timpul necesar pentru parcurgerea unui drum este proportional cu lungimea sa. Se cere sa se realizeze programul pentru determinarea traseului pe care se poate merge intre doua orase date, intr-un timp minim.

(12) Benzinariile

Un sofer doreste sa conduca din orasul A in orasul B, intre care distanta este de n * 10 km (n numar intreg >=1). Incepand cu punctul de plecare A (inclusiv) exista benzinarii (numerotate incepand cu 0) la fiecare 10 km. Masina soferului consuma 1 litru de benzina la fiecare 10 km si are o capacitate a rezervorului de c litri (c numar intreg >=1). Soferul are la dispozitie o harta in care este trecut pretul la fiecare benzinarie.

Sa se scrie un program care sa indice de unde si in ce cantitate trebuie sa cumpere soferul benzina pentru a parcurge drumul cu cost minim, si care este acest cost. Programul va afisa o singura solutie. Initial masina nu are benzina in rezervor, iar de la o benzinarie soferul poate cumpara orice cantitate de benzina, in limitele capacitatii rezervorului.

Programul va citi datele din fisierul a.dat in care pe prima linie sunt trecute, separate de spatii, numerele intregi n si c, iar pe alta linie, tot separate de spatii cele n preturi pe litru la benzinarii (numere reale).

Exemplu:

     Fisierul de intrare:
     5 2
     2.9 3.1 2.8 3.3 2.9
     Iesirea programului:
     Cumpara 2 l de la benzinaria 0
     Cumpara 2 l de la benzinaria 2
     Cumpara 1 l de la benzinaria 4
     Cost total: 14.3

(13) Numere mari

Sa se implementeze un TDA "numere mari". Un "numar mare" este un intreg care poate avea pina la 200 de cifre. Pentru reprezentarea interna a numerelor se vor folosi siruri de caractere. Asupra acestor numere se definesc operatiile aritmetice (adunare, scadere, inmultire).

Sa se scrie un program care utilizeaza TDA numere, citeste 2 numere si realizeaza operatiile aritmetice asupra lor.

(14) Gambling

Un participant la un joc de noroc porneste avand la start o suma de bani A. La fiecare tura a jocului, jucatorul poate pierde sau castiga o suma in valoare fixa B. Sa se gaseasca toate posibilele variante de desfasurare a jocului(secvente pierdere - castig), astfel incat dupa N runde, jucatorul sa aiba aceeasi suma de bani, A, ca la start.

(15) Mozaic

Imaginea unui mozaic se afla intr-un fisier text, fiecare caracter desemnand culoarea unei placute din mozaic. Pentru simplitate, toate placutele sunt de forma patrata, de aceeasi dimensiune, si nu sunt decat doua culori, reprezentate in fisier prin caracterele 0 si 1. Toate liniile fisierului au aceeasi lungime si nu depasesc 250 caractere. Figurile din imaginea mozaicului sunt formate din grupe de 1 sau mai multe patretele adiacente, de culoare 1. Placutele adiacente au cel putin o latura comuna cu restul grupului.

Scrieti un program care sa ceara, prin dialog de la consola, numele unui fisier(dimensiunea fisierului poate fi oricat de mare - peste 100 de linii), si sa afiseze numarul figurilor gasite in acel fisier.

(16) Labirint 2D

Pentru problema clasica de determinare a tuturor solutiilor de iesire dintr-un labirint 2D sa se scrie programul de aflare a optimului (drumul cel mai scurt de iesire)

(17) Printre statui

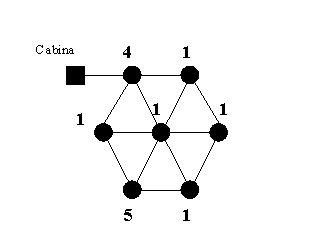
La orele serii, piata centrala in forma de hexagon regulat a orasului X abunda de vizitatori. Atractia o constituie statuile plasate la distante egale si luminate fiecare de un reflector.

La incheierea programului de vizitare, sarcina lui Gogu este de a stinge toate reflectoarele, astfel incat pierderea de energie sa fie minima. El porneste din cabina sa, notata 0, aflata linga coltul din stanga-sus al pietii, revenind in acelasi punct dupa stingerea tuturor reflectoarelor. Se poate deplasa numai pe aleile ce leaga cabina de prima statuie, respectiv statuile intre ele. Aleile sunt de lungimi egale, iar parcurgerea uneia se face intr-o unitate de timp. Poate sa treaca de mai multe ori pe linga aceeasi statuie, la prima trecere stingand reflectorul.

Pregatiti traseul lui Gogu! Daca exista doua variante cu aceeasi energie minima consumata, se va considera solutia care se parcurge intr-un timp mai scurt.

Ca date de intrare, se citesc din fisierul IN.TXT intregii: pe prima linie numarul N al statuilor de pe o latura a pietii, inclusiv colturile, iar pe linia urmatoare consumurile de energie pe unitatea de timp ale reflectoarelor, in ordinea parcurgerii lor pe linii, de la stanga la dreapta.

Se vor afisa: timpul T de parcurgere a traseului, pierderea de energie E si traseul urmat (succesiunea statuilor pe linga care se trece)